Немного о лотереях
В числовых лотереях отдельно взятая простая комбинация равновероятна, и является «единой неделимой сущностью».
Другими словами в пространстве полного массива все элементы (мысленно представим — «кубики»), имеют одинаковый размер, следовательно, нет приоритетных отдельных комбинаций.

Невозможно выделить в полном массиве «универсальные комбинации», которые будут «всегда» играть лучше остальных, так как лототрон или тиражный генератор равновероятен!
Посмотрим, что такое отдельно взятая комбинация на примере лотереи 5 из 36. Всего таких комбинаций в этой лотерее 376 992 штук. Каждая комбинация имеет свой порядковый номер в полном массиве (индекс — ячейку).
Первая комбинация (000001) = 01-02-03-04-05 …
Последняя комбинация (376992) = 32-33-34-35-36 = 376992 штук
[000001] 01-02-03-04-05
[000002] 01-02-03-04-06
[000003] 01-02-03-04-07
[000004] 01-02-03-04-08
…….
…….
…….
[002024] 01-02-07-11-30
[002025] 01-02-07-11-31
[002026] 01-02-07-11-32
…….
…….
[174078] 04-21-25-32-34
[174079] 04-21-25-32-35
…….
[376992] 32-33-34-35-36
Абсолютно любая комбинация в полном массиве ничем не отличается от других в плане вероятности совпадения. Чтобы это лучше понять, нужно представить 376 992 отдельных лотерейных шаров, на которых обозначили все 376 992 комбинации.
Такое количество трудно представить и тем более уместить в картинку, покажу только несколько шаров из 376992 штук.

Проведём мысленный эксперимент — поместим эти шары в огромный лототрон, который выкидывает на каждый тираж только один шар с комбинацией, обозначенной на этом шаре. Не следует забывать, что после каждого прошедшего тиража выпавший шар с обозначенной на нём комбинацией, кидается обратно в этот же лототрон. Таким образом, на следующий тираж все комбинации будут опять на месте, и при запуске лототрона перемешиваться наравне со всеми.
Если трудно представить вариант с шарами, то попробуем представить огромное колесо рулетки, где каждая ячейка для шарика обозначает комбинацию. Таких ячеек 376 992 штук, так как такое разлинованное колесо тоже не получится уместить в картинку, то для общего понимания нарисуем только мизерную часть с комбинациями – выделил начальную и конечную.
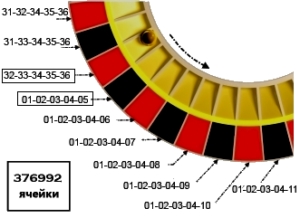
Присмотритесь к рисунку — «колесо» разделено на равные ячейки (равновероятные комбинации), а шарик (тиражный генератор) может попасть в любую лунку (ячейку — индекс), не важно, как мы обозначили эти ячейки (хоть картинками). После тиража (спина) колесо не уменьшается — все ячейки остаются на месте.
- ещё раз обращаю внимание — пишу про целую простую одиночную комбинацию. Для каждой отдельной комбинации (ячейки) полностью теряется смысл, в каких либо чётных, нечётных, суммах, интервалах между числами, повторах, последовательных чисел, и другого – так как комбинация единое целое и обозначает ячейку (индекс) в полном массиве, и их огромное количество.
читать дальше…>>>